2020年以来,物理科学与技术学院统计物理及其交叉学科和多信使天体物理方向已在物理学顶级期刊Physical Review Letters上发表多项重要研究成果,取得了2020年开门红的好成绩。
一、统计物理与复杂系统研究团队在能均分定理和安德森局域化理论研究上取得突破性进展
厦门大学统计物理与复杂系统研究团队赵鸿教授课题组经过多年的潜心研究,近年来在统计物理学的几个基本问题研究上取得了突破性进展。
多体系统的哈密顿函数可以写成如下形式:
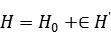
其中第一项为可积哈密顿函数,第二项为非线性扰动,ϵ 是扰动强度。
能量均分定理,即无穷小的非线性扰动能够导致热力学极限系统其能量在各个自由度上均分,是统计物理和凝聚态物理的基础。然而这个定理实际上一直是以假设形式存在的,其严格证明始终未曾得到。证明能均分的努力从上世纪50年代就开始了,其开端是以著名物理学家费米领导的所谓FPUT数值实验,是在当时最大的计算机上进行的。他们惊奇地发现在最基本的一维晶格系统上能量均分没有实现,出现了著名的FPUT回归。基于此“不可接受的结果”,费米至死不同意发表这个研究结果,导致该研究成了学术界最有名的以预印本形式广泛流传的工作,推动了诸多科研领域,如混沌动力学,孤子物理等的发展。
上世纪80年代,大量的数值研究又重新集中到了能均分定理的检验上,这些工作明确了足够大的扰动一定能够导致能量均分。然而原始意义上的能均分,也就是无穷小扰动是否能够导致均分一直没有结论。厦门大学物理系博士生符维成和王振在赵鸿教授和张勇副教授的带领下,以数学物理领域历经几十年所发展出的波湍流理论作为解析工具,结合数值模拟验证,得到一般热力学极限(无穷大)系统能均分时间与扰动强度间存在普适律:
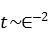
意味着对任意小的扰动,存在一个有限的能达到能量均分的时间阈值,从而首次在严格的意义上证明了经典晶格系统中能量均分定理成立。这些工作已于 2019 年陆续发表[1,2,3]。
利用波湍流理论,课题组再接再厉,对安德森局域化的稳定性这一基本问题首次给出了严格的解析解答。刚刚去世的安德森是凝聚态物理的开创者之一,安德森局域化也是凝聚态物理的核心概念。原始的安德森局域化是在无相互作用的电子系统中推导出来的,安德森局域化在非线性扰动下是否稳定,一直以来都没有明确结论。与传统做法不同,课题组选择了从能均分这一角度来研究安德森局域化稳定性问题,证明了质量无序的非线性晶格系统其能量均分仍然遵从前面得到的普适律,意味着在经典的一维无序系统中安德森局域化是不稳定的,能够被无穷小的非线性扰动所破坏。这一结果刚刚被著名物理学期刊Physical Review Letters接收发表[4],三个审稿人均予以高度评价,认为解决了一个挑战性的问题,将推动一系列相关问题的研究。
参考文献:
[1] Universal scaling of the thermalization time in one-dimensional lattices, W. Fu, Y. Zhang, H. Zhao, Physical Review E 100, 010101 (2019).
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.100.010101
[2] Universal law of thermalization for one-dimensional perturbed Toda lattices, W. Fu, Y. Zhang, H. Zhao, New Journal of Physics 21, 043009 (2019).
https://iopscience.iop.org/article/10.1088/1367-2630/ab115a/meta
[3] Nonintegrability and thermalization of one-dimensional diatomic lattices, W. Fu, Y. Zhang, H. Zhao, Physical Review E 100, 052102 (2019).
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.100.052102
[4] Wave-turbulence origin of the instability of Anderson localization against many-body interactions, Z. Wang, W. Fu, Y. Zhang, and H. Zhao, Phys. Rev. Lett. (2020)(accepted)
https://journals.aps.org/prl/accepted/5d075Y81Wff12b6ef1c062083894a60687910f49c
二、统计物理与复杂系统研究团队在输运问题研究上获得创新性发现
日常生活经验和物理直觉告诉我们热流总是从温度高的地方往温度低的地方流,粒子流则总是从高浓度的地方向低浓度的地方流。然而,令人感到不可思议的是,情况并非总是如此。厦门大学物理系统计物理与复杂系统研究团队王矫教授课题组与合作者发现存在这样的情形,即或者是热流,或者是粒子流,可以沿着与温度和浓度二者均升高的方向流。该研究结果近期发表在国际顶级物理学术期刊Physical Review Letters上[详见Phys. Rev. Lett. 124, 110607 (2020)]。
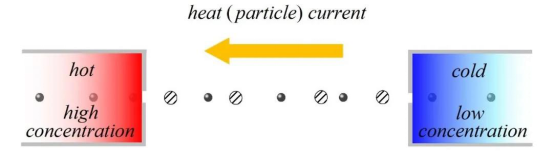
该论文所报告的研究结果与人们一般直觉完全相反,并且,初听上去似乎与热力学基本定律甚至是牛顿运动方程相矛盾。的确,当只有一个热力学力施加于系统上时,由其引发的流必定不能反向,这是由热力学第二定律所保证的。但是,当作用于系统上的热力学力不止一个时(例如,当系统同时存在温度梯度和化学势梯度时),热力学第二定律所施加的限制就不能保证每个流都沿正向流动了。
本文首次在一个具体的物理系统中证明了反向流的存在。对于这个具体的系统,反向流的产生源于其奇特的自组织及非平衡态相变性质。该系统的自组织及非平衡态相变性质也是王矫教授与合作者最先于2017年发现的[Phys. Rev. Lett. 118, 040601 (2017)]。
王矫教授为福建省闽江学者特聘教授,主要从事经典不可积系统的量子力学性质以及近平衡态系统的弛豫及输运问题等方面的科学研究工作,已在Physical Review Letters上发表多篇论文。
原文链接:
J. Wang, G. Casati, G. Benenti, Inverse Currents in Hamiltonian Coupled Transport, Physical Review Letters, 124 (2020) 110607.
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.110607
三、宇宙早期宇称是否守恒?利用星系角动量来检验
自然界曾被认为是简单、对称的。1956年,李政道与杨振宁提出弱相互作用中的宇称不守恒,并获得诺贝尔物理学奖。既然对称性在微观尺度被完全破坏,那么在宏观的宇宙呢?宇宙早期微观尺度的对称性破缺(parity violation)会不会在今天的天体物理尺度上留下可观测的印记?为了解答这些令人好奇的问题,厦门大学天文系于浩然副教授与合作者通过宇宙大尺度结构来重构宇宙早期可能出现的对称性破缺,如手性(chirality)不对称、螺旋性(helicity)不对称。此项研究:Yu, Hao-Ran et al., “Probing Primordial Chirality with Galaxy Spins”于2020年3月10日发表于Physical Review Letters, 124, 101302.
宇宙大尺度结构是人类观测到的星系在宇宙空间中的三维分布。星系在空间的数密度对应宇宙早期的原初密度扰动。针对对称性的测量需要一定的自由度。密度场是标量场,其唯一的自由度不足以携带任何手性和螺旋特征。幸运的是,人类观测到的数百万个星系不仅有位置分布,还有角动量。这些星系的角动量场是矢量场,有三个自由度,携带了额外的大尺度结构及早期宇宙的信息。该论文通过观测星系角动量可以来研究宇宙早期的结构和不对称性。
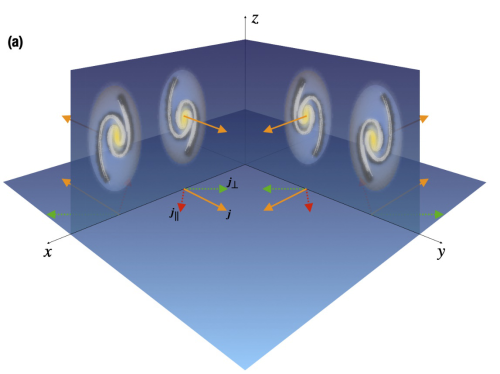

如何观测星系角动量 —— 图(a):通过观测盘星系(薄盘近似)在天空的投影椭圆可以推测出星系旋转的角动量方向的四种可能性。为消除这四种角动量方向的简并,还需要观测旋涡星系的旋涡“缠绕”方向,分别为“S”型或“Z”型,以及星系盘的颜色梯度,如图(a)所示。绝大多数星系向旋臂“凸”的方向旋转,且在远离观测者的方向呈现更多的尘埃消光(颜色偏红)。另外,谱线的Doppler效应也可以测量星系的旋转方向。图(a)橙色箭头表示了星系的角动量方向,红色/绿色箭头表示沿视线平行/垂直方向的角动量方向。
三维矢量场如何携带螺旋特征 —— 螺旋性是矢量场与其自身的旋度的平行性的性质。若矢量场反平行于其旋度,或二者的内积为负,则称左旋,反之为右旋(DNA双螺旋为右旋,大多数海螺、螺丝钉为右旋,右旋的镜像为左旋)。在数学上将矢量场分解为与其旋度反平行(左旋)、平行(右旋)和垂直(散度)的三部分。其中散度部分是E(电场、标量)模式,而左旋和右旋的和是B(磁场)模式。在Fourier空间求解旋度算符(▽×)的本征方程,得到三个本征值和本征矢量,并构成对应的投影矩阵。这三个投影矩阵可将原矢量场分解为E模式、左旋和右旋模式。后两者在Fourier空间振幅(功率谱)的统计不对称是螺旋性的体现。在Fourier空间k标量的螺旋功率谱不违反宇宙学原理,即矢量场满足均匀和各向同性。
重构早期宇宙的信息 —— 为回答有关早期宇宙的问题,需要观测那些与原初宇宙结构的信息线性相关的观测量。太小尺度的恒星、行星甚至世间万物,都经历了高度非线性的过程,与宇宙早期的结构相关性很低;宇宙微波背景辐射、星系分布和大尺度结构仍然包含宇宙早期结构的信息。星系的旋转方向和其所在的暗物质晕(dark matter halo)的角动量方向高度相关,而暗物质晕在Euler空间和Lagrangian空间(即宇宙初期的protohalo)也呈现角动量方向的高度相关,而后者可以很好地被宇宙早期的潮汐扭动理论(tidal torque theory)描述。所以,在Lagrangian空间的星系角动量是早期宇宙结构的探针。
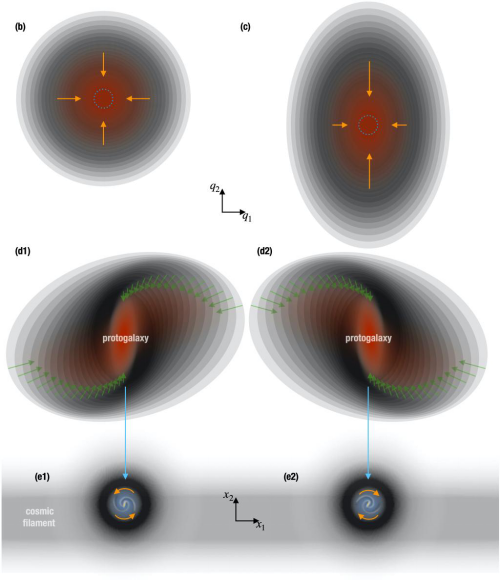

潮汐扭动(tidal twist)—— 星系分布可重构宇宙原初密度场。该论文提出利用密度(潮汐)场信息重构原初角动量信息(spin mode reconstruction),并验证了其与星系/暗物质晕的可观测角动量的相关性。潮汐场,即密度场的逆Laplace算子的Hessian矩阵。图(b-e)中展示了二维空间的宇宙中潮汐与星系角动量的联系,其中椭圆的长轴和短轴表示潮汐张量的两个本征轴,椭圆的大小对应于相应(平滑)尺度的潮汐。(b)中各向同性且不依赖于尺度的潮汐场导致球(圆)塌缩,不产生角动量;(c)中各向不同性、但尺度无关的潮汐导致椭圆塌缩,不产生角动量;(d)中不同尺度潮汐场的本征轴(绿色箭头表示潮汐主轴)随尺度变化,大尺度的潮汐场扭动小尺度的原星系(protogalaxy),产生角动量spin mode,并在(e)中的宇宙纤维结构(cosmic filament)中形成两个角动量相反的星系。(d1,e1)和(d2,e2)互为镜面反演;这种奇宇称(parity-even)的可观测量可被原初偶宇称(parity-even)的密度场(标量)及潮汐场(对称张量)预测,因此这个可观测的角动量也是早期宇宙的探针。早期宇宙的宇称破缺可能会通过这种spin mode携带到今天星系的角动量场。该论文Conclusion and discussion中及相关参考文献给出了可能的对称性破缺机制。
该论文第一作者和通信作者为天文系副教授于浩然,南强青年拔尖人才计划支持的特任研究员。此项工作得到了国家自然科学基金青年科学基金项目NSFC11903021的支持。
文章链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.101302